Diffraction Physics: Fresnel & Fraunhofer

How Scientists Uncovered Two Faces of Diffraction

When early physicists like Huygens, Young, and Fresnel studied light, they noticed something unusual: Light didn't only travel straight — it bent around edges and created unexpected shadow patterns.

But these patterns changed drastically depending on how close the obstacle and screen were. Scientists realized that one mathematical model couldn't explain both situations.

Interactive Diffraction Simulator

Aperture Parameters

Aperture Size (a):

200 μm

Distance (L):

300 mm

Wavelength (λ):

550 nm

Aperture Type

Fresnel Number: 0.61

Fraunhofer Regime (F < 1)

The key parameter that determines the diffraction regime is the Fresnel Number:

$ F = \frac{a^2}{L\lambda} $

Where $a$ is the aperture size, $L$ is the distance to the screen, and $\lambda$ is the wavelength of light.

Fresnel Diffraction ($F \gg 1$): Near-field, complex patterns
Fraunhofer Diffraction ($F \ll 1$): Far-field, Fourier transforms

Fresnel Diffraction

Near-field patterns where wavefronts are curved and patterns are irregular.

Key Characteristic

Occurs when source, slit, or screen are close to each other.

Fraunhofer Diffraction

Far-field patterns where wavefronts are flat and patterns are stable.

Key Characteristic

Occurs when light source and screen are at large distances.

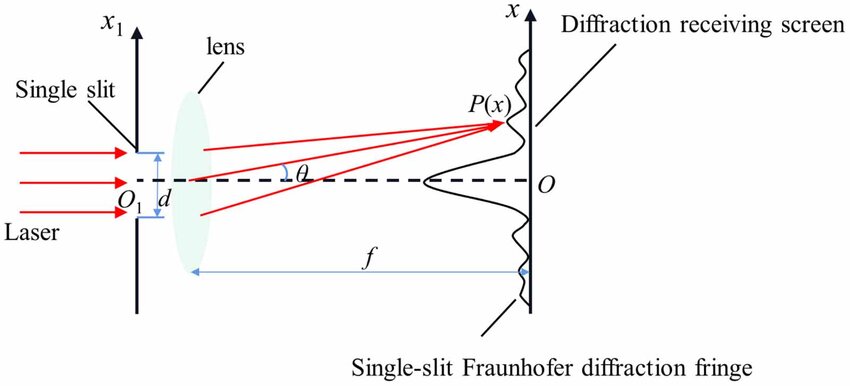
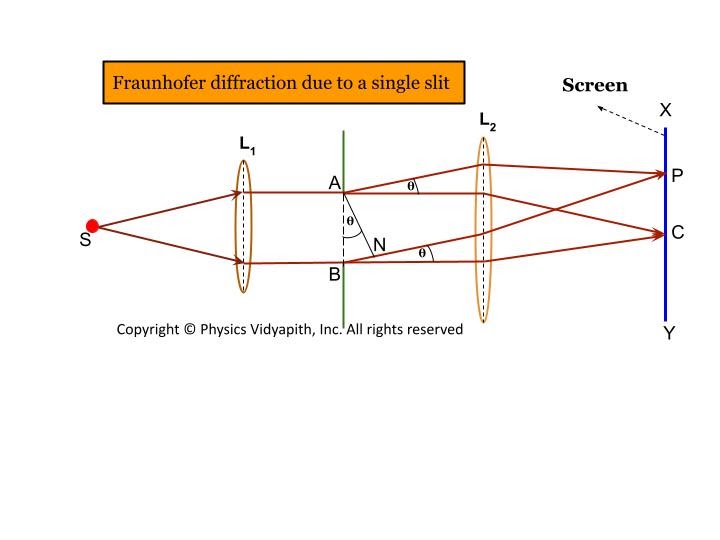
Fresnel Diffraction — Light Behavior in the Near Field

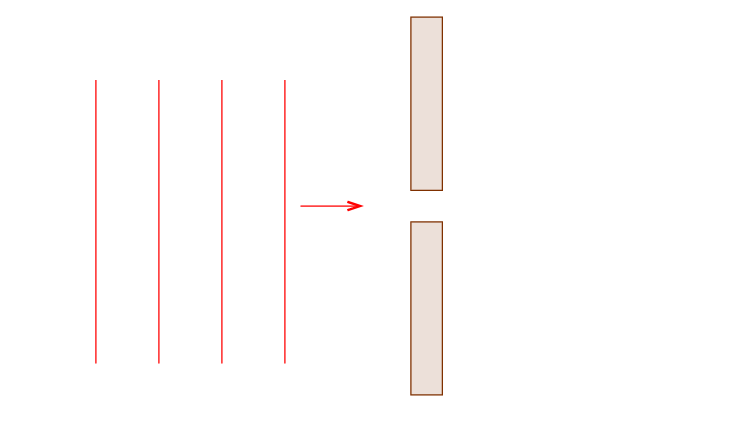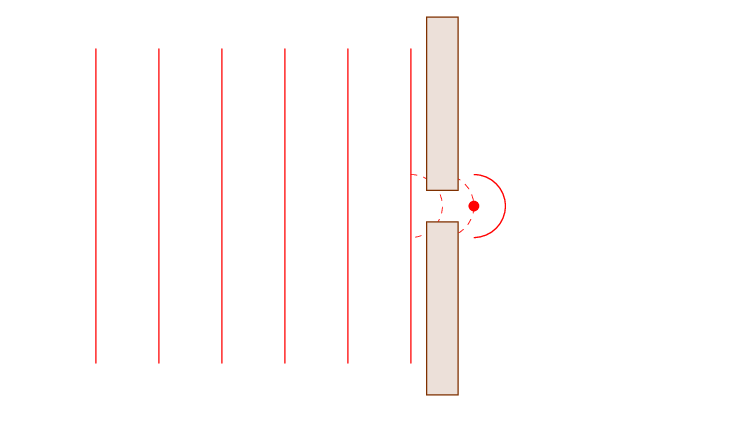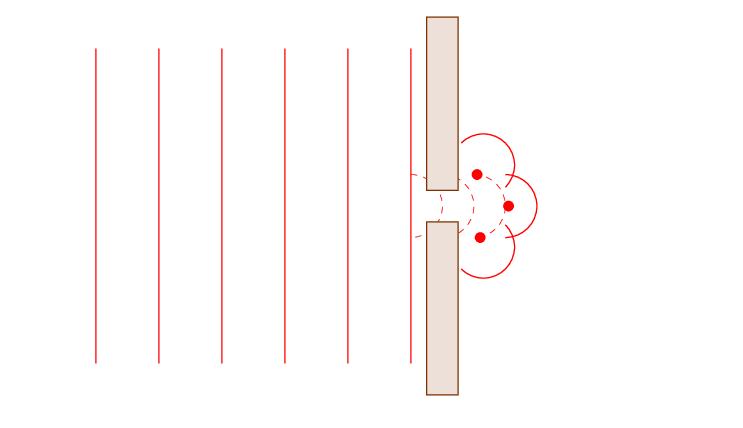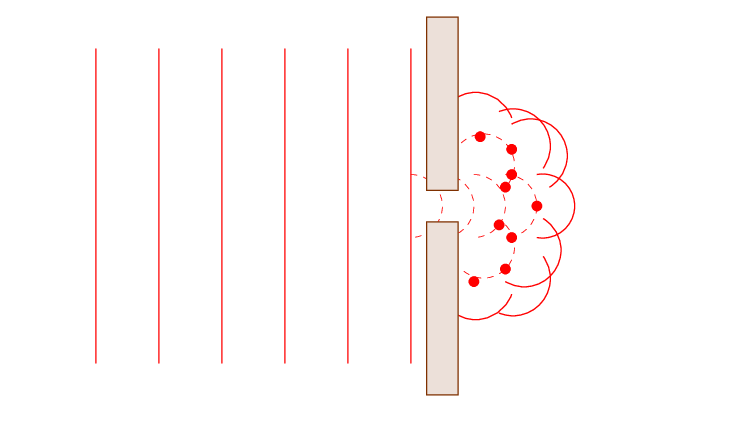
Proposed by Augustin-Jean Fresnel while proving the wave nature of light, Fresnel diffraction occurs when the source, slit, or screen are close to each other.

Key Concepts

Curved Wavefronts

Wavefronts reaching the slit are curved, not flat.

Irregular Patterns

Diffraction pattern changes with distance and appears irregular.

Reorganizing Light

Light is still reorganizing its wavefronts.

Real-Life Implementations

The soft edges of shadows around everyday objects
Fresnel lenses used in projectors and lighthouses
Optical security designs (holograms, VR lenses)
Diffraction around buildings, edges, and coins

$Fresnel near-field diffraction$

Fraunhofer Diffraction — Light Behavior in the Far Field

Developed by Joseph von Fraunhofer, who studied light using prisms and diffraction gratings, Fraunhofer diffraction occurs when the light source and screen are at a large distance, or lenses convert the waves into parallel rays.

Key Concepts

Plane Wavefronts

Incoming wavefronts become plane (flat), simplifying calculations.

Stable Patterns

Produces a clean, stable, symmetric diffraction pattern.

Final Pattern

Light has traveled far enough that wave curvature disappears.

Real-Life Implementations

Spectrometers and wavelength measurement
Diffraction gratings (CD/DVD rainbow colors)
Telescope & microscope resolution calculations
Laser beam shaping and optical communication

$Fraunhofer single-slit diffraction diagram$

$Fraunhofer single-slit diffraction photograph$